浅谈树状数组
树状数组是一种功能类似线段树的数据结构,但在代码量上较线段树更少,也同样能进行对序列的修改与查询操作。

什么是树状数组?
树状数组, 或 Binary Indexed Tree(也称 Fenwick Tree ),是一种能够高效更新并计算数列前缀和的数据结构。
树状数组的实现主要基于计算二进制 lowbit(也就是值为
原理
既然树状数组与线段树类似,我们不妨将线段树的实现方式先搬过来看看。对于一个表示数列
也就是说,在线段树中每一个非叶子结点都管理着当前孩子结点的信息。这种操作的具体实现就是 pushup 操作。这样在查询时,我们只需要找到对应的父亲节点即可。
而树状数组所使用的策略与线段树几乎别无二致:同样适用父亲节点来表示其孩子节点的信息,且同为递归定义。同样地,在查询时只需要查询所属叶子结点的父亲节点即可。显然,对于根节点将会管理数列中的所有节点的信息。
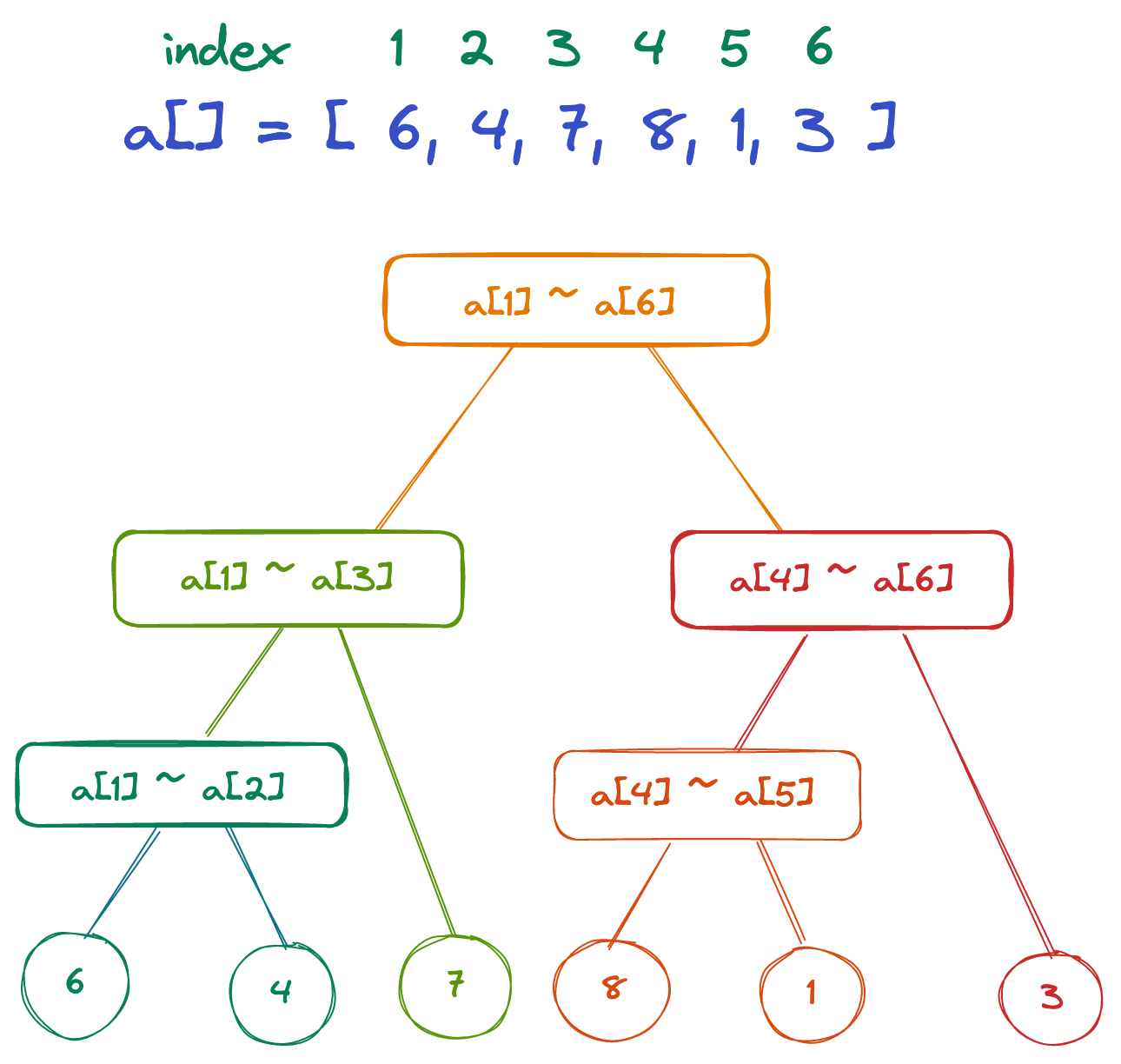
上图就是一个典型的使用树状数组维护出来的树形结构。最上方的 a[] 表示数据数组,一一对于最下方的叶子结点(圆圈)。每一个父亲节点都使用方形表示,控制着至少两个结点。
将上图中的结点进行编号,得:
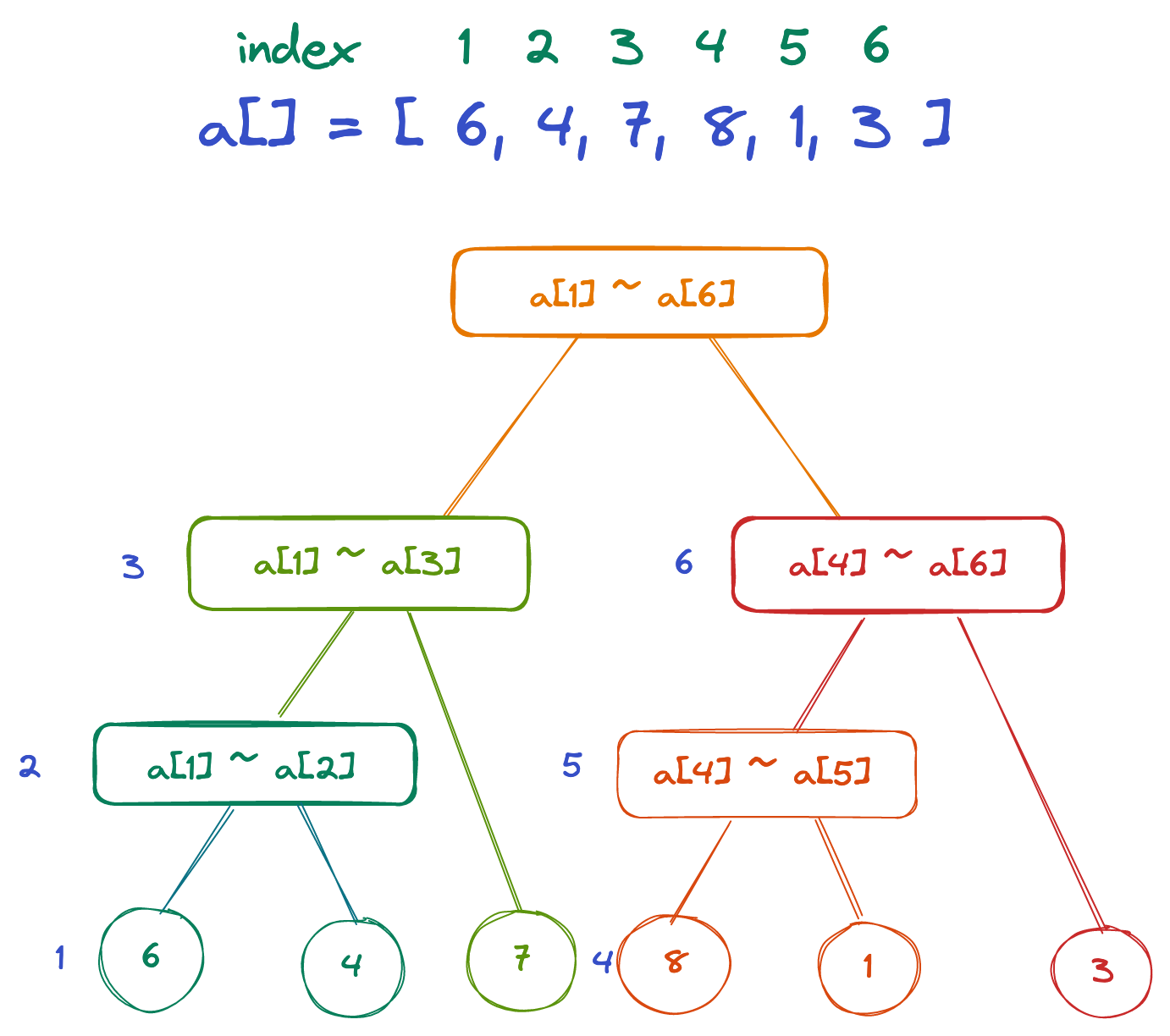
每个节点右面的蓝色数字为当前节点的编号。如果将树状数组表达为
考虑计算下述表达式:
对于修改操作,我们也可以采用类似的思想。修改操作无非就是将给定的增加值依次向上更新传递。例如,将
对于
实现
注意到上述所有操作都依赖于一个重要操作:求某数 lowbit :
int lowbit(int x) {
return x & -x;
}
该函数的返回值即为
- 若
,则其补码为 , = 。 - 计算
x & -x,结果为。 - 验证上述操作,
的二进制最低 的位置从零开始计数为 , ,结果正确。
于是我们便不难写出模板代码:
template <typename T = int>
class FenwickTree {
private:
T tr[N];
int lowbit(int x) { return x & -x; }
public:
void add(int x, T k) {
while (x <= N) {
tr[x] += k;
x += lowbit(x);
}
}
T prefix_sum(int x) {
T ans = 0;
while (x >= 1) {
ans += tr[x];
x -= lowbit(x);
}
return ans;
}
T sum(int l, int r) {
return prefix_sum(r) - prefix_sum(l - 1);
}
};
不难发现虽然基本操作是前缀和,但仍然可以使用两个前缀和的差求出任意区间和。值得注意的是,虽然 lowbit 函数仅支持整数操作,但树状数组支持任意数据类型:lowbit 维护的是数组下标,并不对实际内容进行操作。
不难发现求和与修改操作都是
对比线段树,我们发现树状数组并不能很高效地处理区间更新问题。注意到原本的前缀和操作,我们不妨将其改为差分操作。这样,每次存储
这样,对于修改操作我们只需要对
尽管无法直接进行区间求和的维护操作,我们仍可以通过维护两个树状数组的方式同时进行区间修改与区间查询的操作。参考 OI-Wiki 。但是本人认为进行这样的操作不如使用线段树方便。
例题:https://www.luogu.com.cn/problem/P3368 。
显然对于这道题,我们需要进行区间修改与单点查询。参考代码如下:
// Problem: P3368 【模板】树状数组 2
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3368
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <memory.h>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <iostream>
#include <queue>
#include <stack>
#include <string>
#include <vector>
using namespace std;
const int N = 5 * 1e5 + 10;
int bit[N], n, m, x, y, k, op, a[N];
int lowbit(int x) { return x & -x; }
void add(int x, int k) {
while (x <= n) {
bit[x] += k;
x += lowbit(x);
}
}
int prefix_sum(int x) {
int ans = 0;
while (x >= 1) {
ans += bit[x];
x -= lowbit(x);
}
return ans;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
add(i, a[i] - a[i - 1]);
}
for (int i = 1; i <= m; i++) {
cin >> op;
if (op == 1) {
cin >> x >> y >> k;
add(x, k);
add(y + 1, -k);
} else {
cin >> x;
cout << prefix_sum(x) << endl;
}
}
return 0;
}
注意到核心模板代码无需改变。
总结
不难发现,朴素树状数组可以进行大部分线段树可以进行的操作:区间求和与单点更新、区间修改与单点查询。但是,这两组操作却无法使用一个树状数组同时实现。简单来说,树状数组能做的操作线段树也一定能做,但反之却不亦然。
在对于高级操作没有要求的题目下,使用树状数组是一个很好的选择,因为其代码复杂度明显较低。但在复杂的题目时,线段树会略胜一筹。
值得注意的是,虽然线段树与树状数组时间复杂度相同,但树状数组常数略小。在更新操作时,树状数组不一定一定要遍历
总之,哪个好用用哪个。