什么是堆？

堆是一种特殊的树，其每个节点都有一个权重 $w_i$ ，且每个节点的权重 $w_i$ 均小于/大于其父亲节点。

上图就是一个典型的堆。如果每个节点的权重都 $\geq$ 其父亲节点的权重，那么这个堆就是一个小根堆，反之则是大根堆。不难发现，上图是一个小根堆。

我们今天所要讨论的二叉堆则是一个用数组维护的完全二叉树，也适用于上述规则。

C++ STL 中的 priority_queue 就是一个典型的堆。

堆的操作

插入

给定一个合法的堆 $H$ ，现在需要插入一个权值为 $x$ 的元素到 $H$ 中，这就是插入操作。还是上面的那棵树，现在我们希望加入一个元素 $5$ 到堆里：

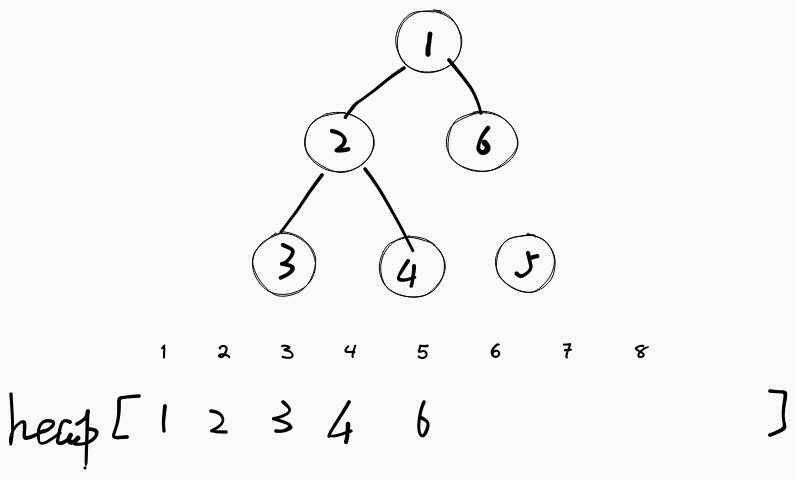
下方的数组表示当前堆的存储情况。很显然我们可以先随便把这个节点加到堆里，然后再想办法维护整个堆使其合法。那么我们将新节点先挂载到节点 6 的位置（数组下标），然后考虑如何进行维护。

显然对于当前节点无非就有两种情况：

1. 当前节点小于父亲节点，需要向上移动；
2. 当前节点大于等于父亲节点，无需移动。

那么我们就可以一直向上移动新节点直到满足情况 (2) 时为止。

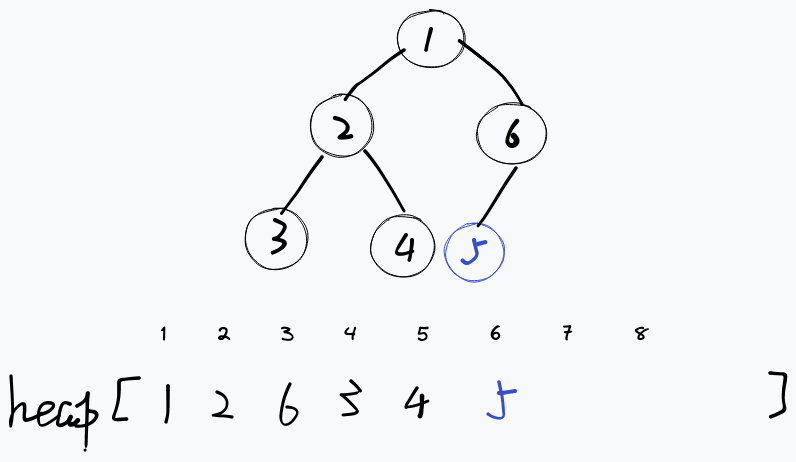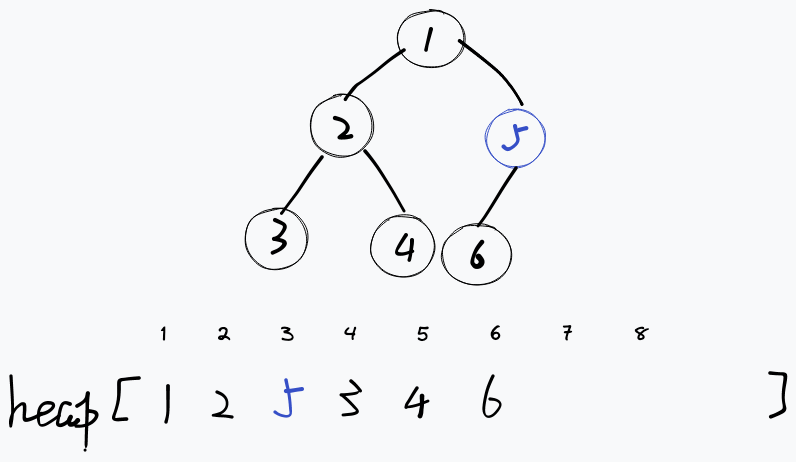
对于这个堆，我们只需要将新节点向上移动一层即可。这个操作就叫做 向上调整 ，或 Decrease Key ，代码如下：

// 向上调整操作，x 为需要进行调整位置的元素下标
void up(int x) {
  while (x > 1 && H[x] < H[x / 2]) {
    // 遇到不合法的就交换父亲节点与当前节点
    swap(H[x], H[x / 2]);
    x /= 2;
  }
}

// 插入操作，x 为需要插入的值
void insert(int x) {
  n++;
  H[n] = x;
  up(n);
}

该算法的时间复杂度为 $O(\log n)$ ，其中 $n$ 为节点数。证明显而易见，up() 函数中的 while 循环最多执行 $k$ 次，其中 $k$ 为堆的高度。显然，$k = \log n$ 。

删除

删除操作将会删除当前堆的根节点，在我们的堆中也就是最小的元素。很明显我们没办法直接删除根节点，因为那样会导致整个堆变成两个堆。我们不妨考虑将根节点与最后一个节点互换，然后再像插入操作那样想方设法维护这个堆使其满足性质。

很明显交换、删除根节点后的堆可能不满足我们小根堆的性质，也就是根节点可能比孩子节点还要大。那么我们就可以按照向上调整的思路，写出 向下调整 ，来维护我们的堆。

对于向下调整，我们从当前节点的子节点中找到一个最小的元素互换，一直重复此操作到最下层。

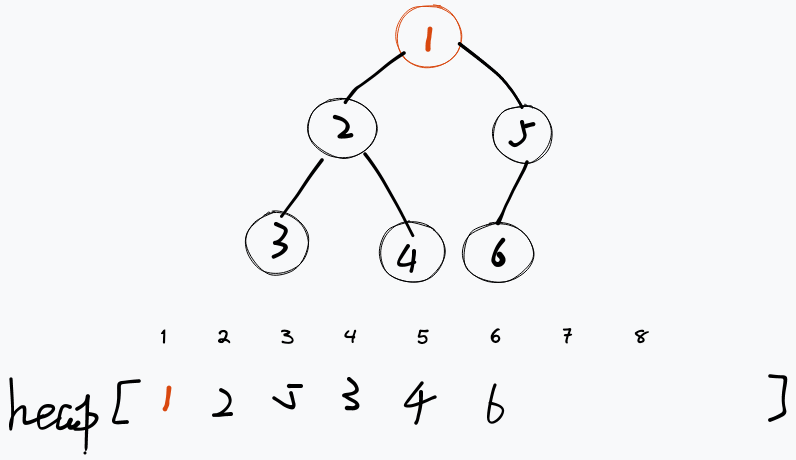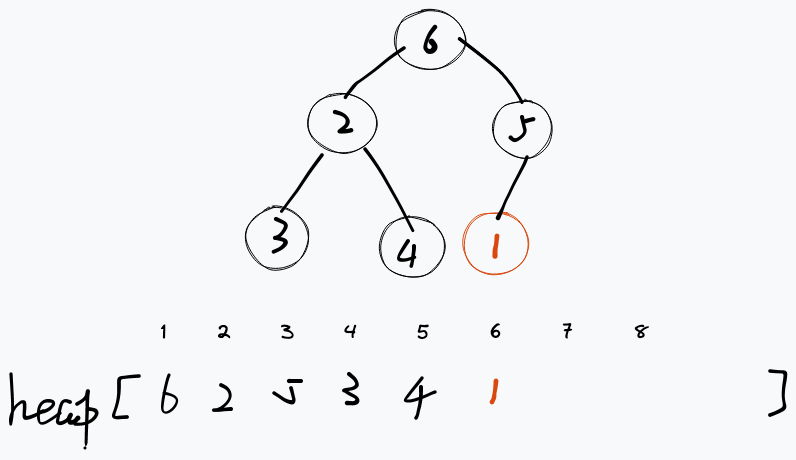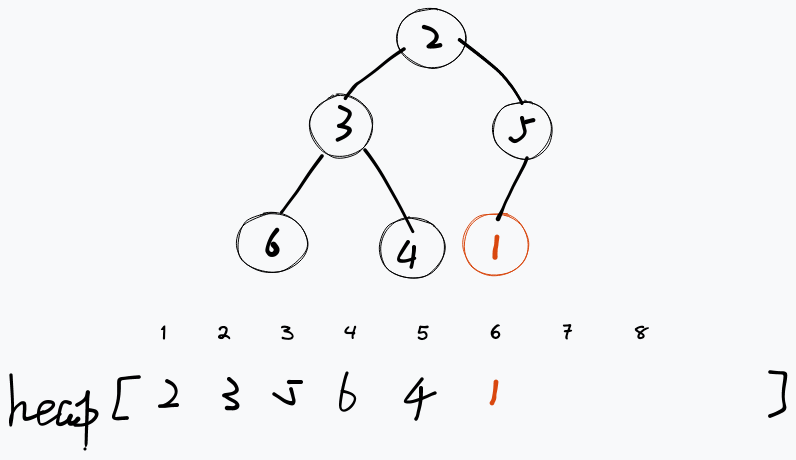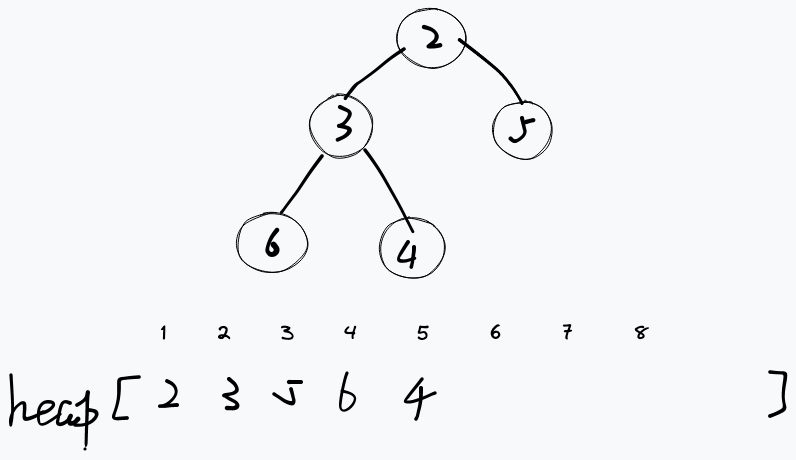
参考代码：

// 向下调整操作，x 为需要调整的下标
void down(int x) {
  while (x * 2 <= n) {
    int cur = x * 2;
    if (cur + 1 <= n && H[cur + 1] < H[cur]) cur++;
    // 当前子树根节点符合条件意味着子树的子树也符合条件了
    if (H[cur] <= H[x]) break;
    swap(H[cur], H[x]);
    x = cur;
  }
}

// 删除根节点操作，返回原根节点的值
int remove() {
  int ret = H[1];
  H[1] = H[n], n--;
  down(1);
}

删除操作的时间复杂度同样为 $O(\log n)$ ，其中 $n$ 为元素个数。证明同插入操作。

查询

查询操作能够查找当前堆内的最小（或最大，依据大小根）元素。这可能是所有二叉堆操作中最没有脑子的一个了……直接返回根节点即可。代码如下：

// 查询操作，返回当前堆内最小值（根节点）
int query() {
  return H[1];
}

显然时间复杂度为 $O(1)$ 。

建堆

基本的增删改查操作有了，接下来就是如何从一个一直序列中转化为堆了。很显然我们可以从空堆开始逐个进行 insert 操作，时间复杂度为 $O(n \log n)$ 。那么，有没有时间复杂度更优的算法呢？

答案是肯定的。如果我们用逆向思维思考整个问题，从最底层的叶子节点开始，进行向下调整的操作，使得当前每个子节点的子树都满足堆的条件。这样，我们变相地合并了两个子堆，从而达到了我们想要的结果。

参考代码如下：

// 建堆操作，a[] 为原始序列，n 为序列长度
void build(int a[], int n) {
  for (int i = 1; i <= n; i++) H[i] = a[i];
  for (int i = n; i >= 1; i--) down(i);
}

该算法的时间复杂度为 $O(n)$ ，关于时间复杂度的证明可以参见 OI-Wiki 或《算法导论》6.3 节。

模板题

链接：洛谷 P3378 堆 。

题目要求增删查三种操作，妥妥的模板。下面给出面向对象版的代码：

// Problem: P3378 【模板】堆
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3378
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <memory.h>

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <iostream>
#include <queue>
#include <stack>
#include <string>
#include <vector>
using namespace std;
const int N = 1e6 + 10;

int n, op, x;

template <typename T, int N = int(1e6 + 10), typename U = less<int>>
class Heap {
   private:
    int size;
    T H[N];
    U cmp = U();

   public:
    Heap() { size = 0; }

    void up(int x) {
        while (x > 1 && cmp(H[x], H[x / 2])) {
            swap(H[x], H[x / 2]);
            x /= 2;
        }
    }

    void insert(int x) {
        size++;
        H[size] = x;
        up(size);
    }

    void down(int x) {
        while (x * 2 <= size) {
            int cur = x * 2;
            if (cur + 1 <= size && cmp(H[cur + 1], H[cur])) cur++;
            if (cmp(H[x], H[cur])) break;
            swap(H[cur], H[x]);
            x = cur;
        }
    }

    int remove() {
        int ret = H[1];
        H[1] = H[size], size--;
        down(1);
        return ret;
    }

    int query() { return H[1]; }

    bool empty() { return size <= 0; }
};

Heap<int> H;

int main() {
    cin >> n;
    while (n--) {
        cin >> op;
        if (op == 1) {
            cin >> x;
            H.insert(x);
        } else if (op == 2) {
            if (H.empty()) continue;
            cout << H.query() << endl;
        } else {
            if (H.empty()) continue;
            H.remove();
        }
    }
    return 0;
}

对顶堆

对顶堆，顾名思义，是一种由一对大小根堆结合而成的数据结构，可用于动态维护序列的第 $k$ 大值，例如动态维护序列中位数等。

【详情待补充】