wjr的有根树 题解
图论 / wjr的有根树 题解

题目描述
说明
wjr 最近学习了《树》的概念
他觉得很有趣,于是自己花了一棵包含 nn 个节点的树,每条边的边长不一定相同,并且自己指定了一个节点
为了让这棵树更加有趣,wjr 把每条边设置成了有向边,这条边只允许从父亲走向儿子
现在 wjr 想知道,这棵树上有多少路径长度为
输入格式
输入第一行包含三个整数 n,p,kn,p,k,如题意所示。
接下来 n-1n−1 行每行包含三个整数 u,v,xu,v,x ,表示节点 uu 和节点 vv 之间存在一条长度为 xx 的边。
对于
对于
对于
输出格式
输出一行,该行包含一个整数,表示答案
样例
输入数据 1
5 2 2
2 1 2
2 3 1
3 4 1
3 5 1
输出数据 1
3
题解
昨天%你赛的题,暴力挂了拿了零分。看了题解之后发现好巧妙,于是诞生了这篇文章。
首先肯定这是一道裸的图论题,求树上权值和为
首先既然是棵树,我们不难想到跟这道题有关的性质:
- 从根节点到树上任意一个点有且仅有一条唯一路径
- 树上不存在环
- 根节点一定能够到达任意一个节点
首先想到的是考虑枚举每个点从它的祖宗节点经过的每条路径(可能有重合)的权值和,但显然
~~考虑到上道题就是滑动窗口,~~考虑使用滑动窗口的方式进行优化。从树上每个叶子节点向上遍历直到根节点的路径是唯一的,所以可以使用树上滑动窗口解决。
具体操作就是找到一个叶子节点后,对从该节点到根节点的这条路径进行滑动窗口,在缩小左端点的同时尽可能缩小右端点。说的形象点就是像蛇一样在这条路径上伸缩,直到总和为
目前为止,一切看起来都还好,只需要实现树上滑动窗口即可。但是,仔细看题可以发现,给定的边并没有指定位置关系:
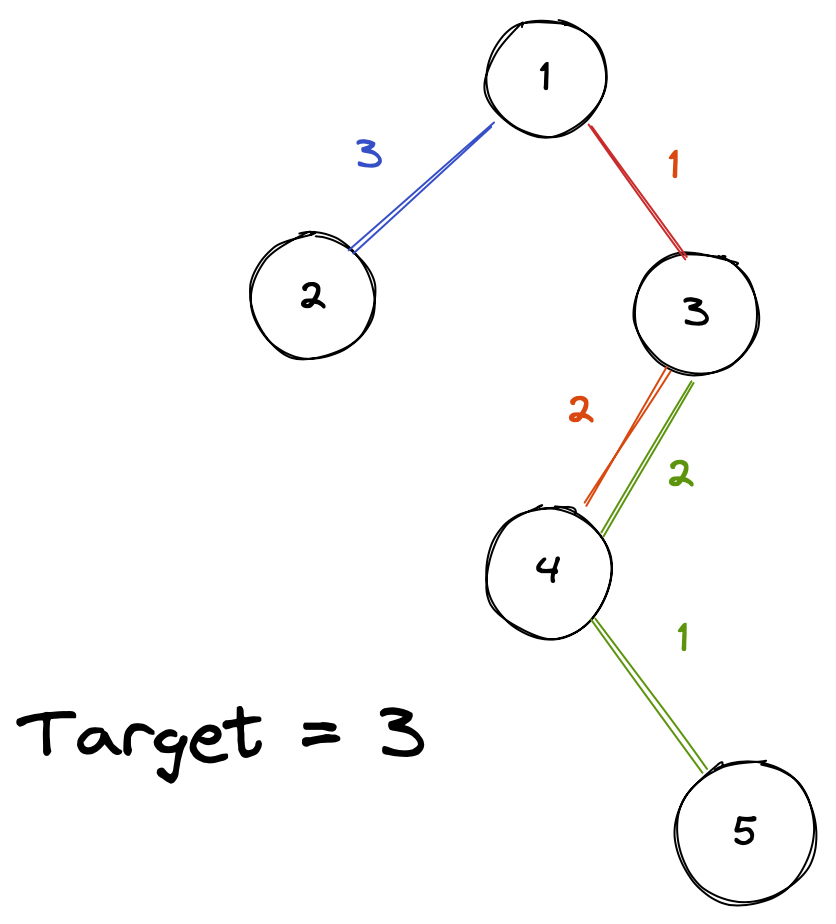
这时,如果配上这样的输入:
5 4 1
3 4 2
1 3 1
2 1 3
我们的算法就会出现错误的结果。解决方案也很简单,建立双向边即可。这就是这道题最大的坑点,也是最巧妙的点。建立双向边之后我们只需要判断是否走重即可。
代码
#include <memory.h>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <iostream>
#include <queue>
#include <stack>
#include <string>
#include <vector>
using namespace std;
const int N = 2 * 1e5 + 10;
struct Node {
int id, w, p;
Node() {}
Node(int _id, int _w, int _p) { this->id = _id, this->w = _w; this->p = _p; }
};
queue<Node> q;
int h[N], vtx[2 * N], nxt[2 * N], w[2 * N], idx, vis[2 * N];
int n, p, k, ans, maxEdge, fa[2 * N], sum[2 * N];
void addEdge(int a, int b, int c) {
vtx[idx] = b, nxt[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void dfs(int prev, int cur) {
fa[cur] = prev;
int p = h[cur];
bool isLeaf = true;
while (p != -1) {
if (prev == vtx[p]) {
p = nxt[p];
continue;
}
isLeaf = false;
sum[vtx[p]] = sum[cur] + w[p];
dfs(cur, vtx[p]);
p = nxt[p];
}
if (isLeaf) {
int l = cur, r = cur;
while (r != p) {
if (vis[l] || sum[l] < k) break;
vis[l] = 1;
while (sum[l] - sum[r] < k) r = fa[r];
if (sum[l] - sum[r] == k) ans++;
l = fa[l];
}
}
}
int main() {
memset(h, -1, sizeof(h));
cin >> n >> p >> k;
for (int i = 1; i <= n; i++) {
int u, v, w;
cin >> u >> v >> w;
addEdge(u, v, w);
addEdge(v, u, w);
}
dfs(-1, p);
cout << ans << endl;
return 0;
}
AC++!